[DRAFT] Garbled Circuits: Commutative Encryption Protocol

Problem definition and a naive protocol

Definition

Alice has secret bits $X = x_0\ldots x_{n - 1}$ and Bob has secret bits $Y = y_0\ldots y_{m - 1}$. Alice and Bob are interested in computing an arbitrary boolean function $f(X,Y)$ so that at the end they both know the outcome, but neither of them learn anything more than the value of $f(X,Y)$.

Relationship to Oblivious Transfer

Oblivious transfer (OT) refers to the case where Alice has a list of values $A$, Bob wants to retrieve an element of $A[i]$ without revealing $i$ to Alice. That is, at the end of the protocol Bob learns $A[i]$ while Alice learns no information about $i$ and Bob learns nothing about the other elements in $A$.

If we have this primitive, then to do two party computation Alice could compute a table $T$, such that $T[i] = f(X,i)$, for $0 \leq i < 2^{m}$. Then Alice and Bob run OT on $T$ and $Y$ so that at the end Bob learns the value $T(Y) = f(X,Y)$, while revealing nothing about $Y$. Then he could share that value with Alice.

Note that the size of $T$ grows exponentially with $m$ making our above protocol impractical for large secrets.

Composing Oblivious Transfers

To avoid performing Oblivious Transfer on prohibitively large tables, we design a protocol for 2-party commutation so that the computation is done via a series of Oblivious Transfer like steps (one per gate). Each transfer only involves a table of constant size, and is done in a way that does not reveal the output of the gate. We present two ways to achieve that:

1. Public Encrypted Values: In this method, we stop the oblivious transfer at the point where the output value is encrypted with the keys of both Alice and Bob ($\hat{M}$ in the diagram above). For intermediate gates, we design protocols that are able to handle if one or both values are encrypted.

2. Shared Secrets: In this method, we make it so that for each intermediate value $x_i$ Alice knows $a_i$ and Bob knows $b_i$ so that $x_i = a_i \oplus b_i$. Oblivious Transfer is used to design gates that operate on pairs of secret values $\left( a_i,b_i \right)$ and produce a pair of secret values (so that only Alice knows $a_i$, and only Bob knows $b_i$).

Composing Public Encrypted Values

As discussed in the previous section, when computing a single gate where a bit of the input is known by Alice, and another is known by Bob. Then Alice makes a table of the output of the gate depending on Bob’s value, and then Alice and Bob perform an oblivious lookup on the table to get the output of the gate. However, they stop at the step where the output is encrypted with both their keys. For the rest of this section we discuss how we can compute the output of intermediate gates where one or two of the inputs is encrypted.

Handling a single encrypted input

Motivation

Let’s say that we are interested in computing $a \oplus e$, where Alice knows $a$, and $e$ is an intermediate value that’s encrypted in both Alice and Bob keys. It seems intuitive that we would want Alice to compute the output of this gate, since knowing $a$ it’s easier for her to compute the output in terms of $e$; for example, if $a = 0$, then $\mathsf{out} = e$. However, the issue is that if $a = 1$ then $\mathsf{out} = \overline{e}$. So unless the encryption has some special properties, computing the output might be challenging for Alice based solely of the encrypted value $e$. To get around this, we give Alice access to three extra things. The encryption of $\overline{e}$ which must be computed at the output of the previous gate. As well as valid encryption in Bob’s keys for $\mathop{\text{Enc}}_{K_{b}}(0)$, $\mathop{\text{Enc}}_{K_{b}}(1)$ which they can share once at the beginning. This is motivated by the following lemma:

Lemma: For any binary gate $f(a,b)$, knowing $a$, the output is always either $1$, $0$, $b$ or $\overline{b}$.

Proof. There are two cases:

• If $f(a,0) = f(a,1) \in \left\{ 0,1 \right\}$, then we can use $0$ or $1$.
• If $f(a,0) = \overline{f(a,1)}$, then we can use $b$ or $\overline{b}$. $\square$

Construction

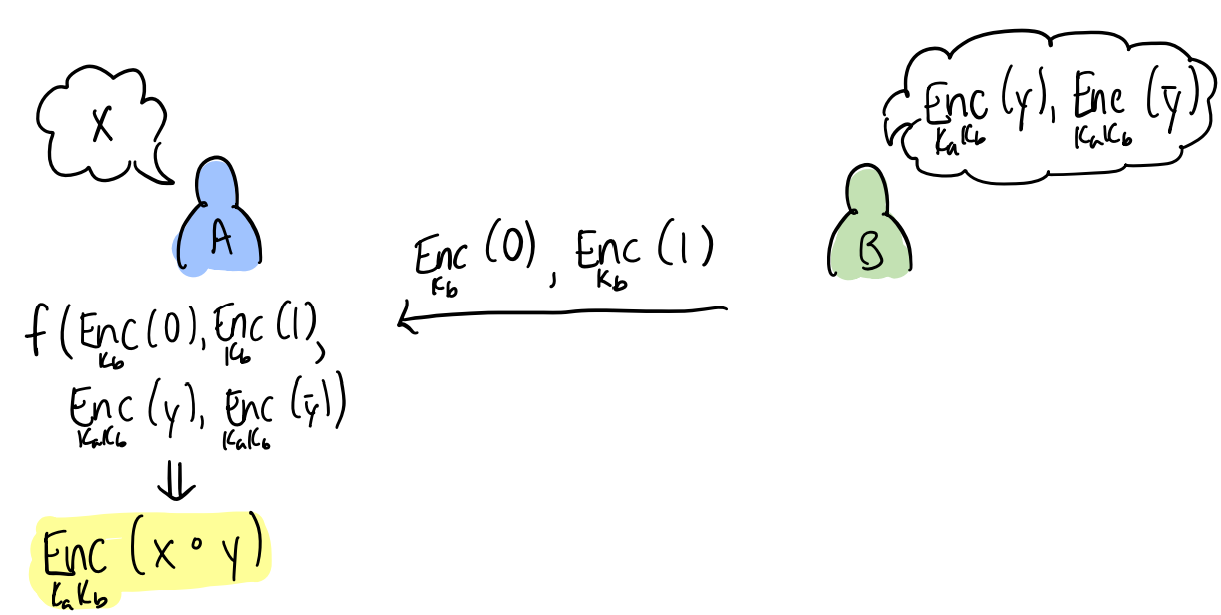
1. At the beginning, each of Alice and Bob share valid encryption of $0$ and $1$ in their keys. (We are using IND-CPA secure encryption schemes.)

2. When running secret sharing in gates that only take as input values that are known to either Alice or Bob, we produce both $\mathop{\text{Enc}}_{K_{A},K_{B}}(\mathsf{out})$, $\mathop{\text{Enc}}_{K_{A},K_{B}}\left( \overline{\mathsf{out}} \right)$. (This can be done by replacing each entry in the table with a pair.)

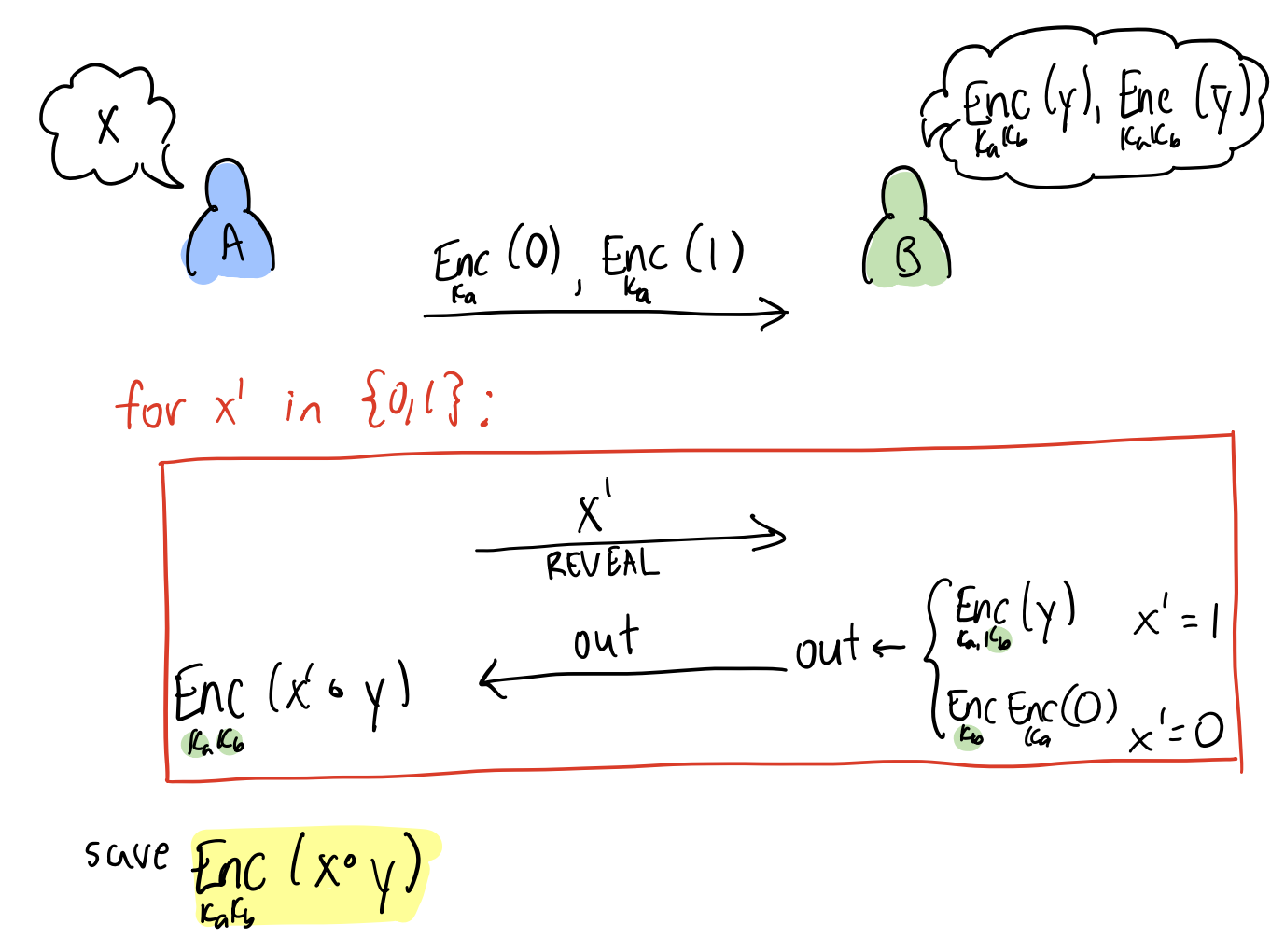
3. When one of the inputs to the gate is a shared encrypted value ($\mathop{\text{Enc}}_{K_{A},K_{B}}(x)$, $\mathop{\text{Enc}}_{K_{A},K_{B}}\left( \overline{x} \right)$ for some $x$), and the other is known by Alice. Then Alice can compute the output purely from $\mathop{\text{Enc}}_{K_{A},K_{B}}(x)$, $\mathop{\text{Enc}}_{K_{A},K_{B}}\left( \overline{x} \right)$, $\mathop{\text{Enc}}_{K_{A},K_{B}}(0)$, $\mathop{\text{Enc}}_{K_{A},K_{B}}(1)$. To prevent Bob from learning anything, Alice needs to re-randomize the encryption before producing the output. (This can be accomplished by decryption and re-encrypting with her key).

To motivate the next protocol, we can alternatively have Alice offload the work to Bob with the following protocol:

Handling two encrypted inputs

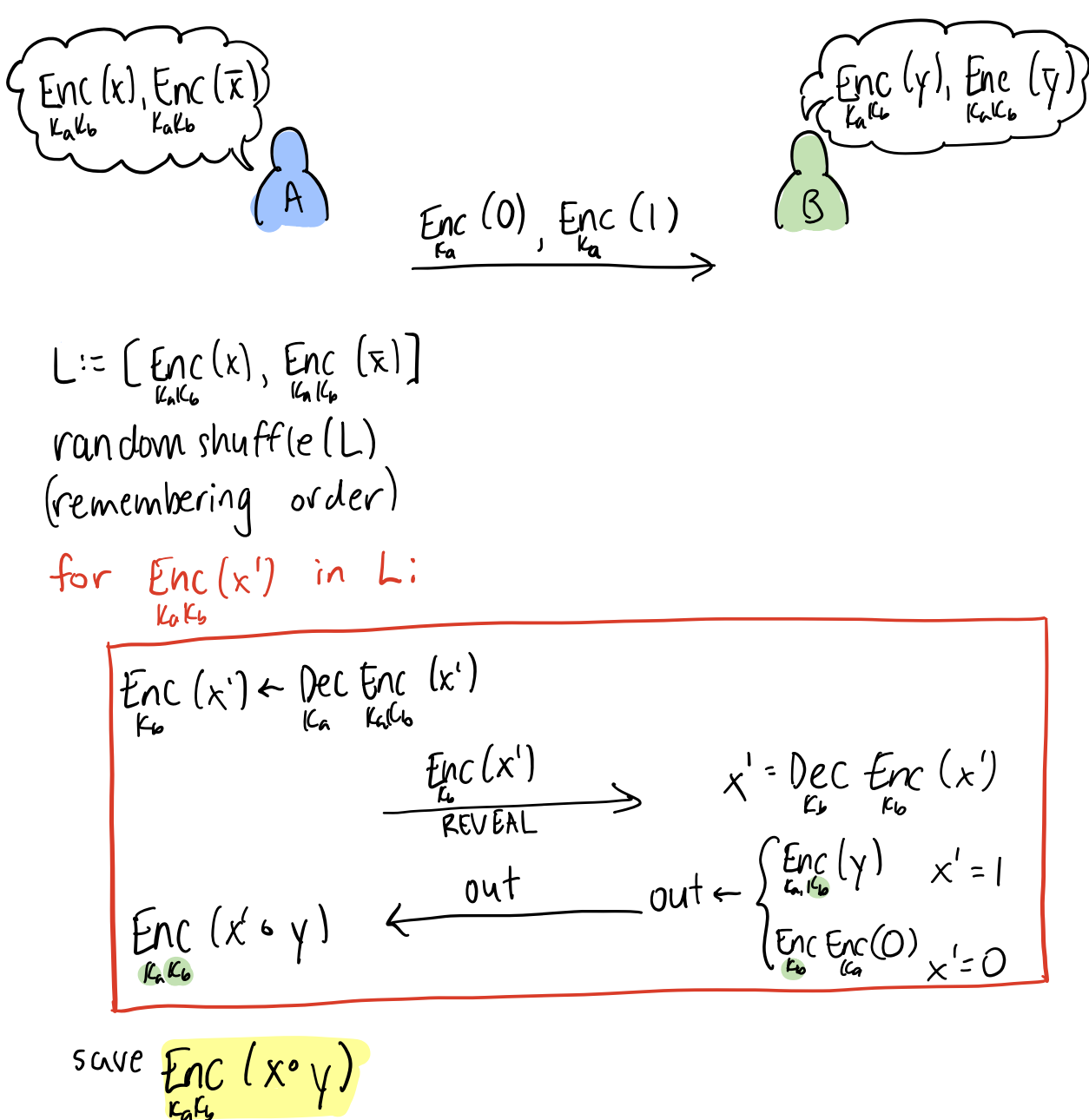
We reduce this case to the previous, by having one of the parties (Alice) reveal one of the secrets to the other (Bob). However, in order to prevent Bob from learning the value of the encrypted input $\mathsf{enc}$, she reveals $\mathop{\text{Enc}}_{(a,b)}(x)$ and $\mathop{\text{Enc}}_{(a,b)}\left( \overline{x} \right)$ to him in a random order. Bob computes the encrypted outputs $\mathop{\text{Enc}}_{(a,b)}(y)$, $\mathop{\text{Enc}}_{(a,b)}\left( \overline{y} \right)$ assuming both values; then Alice re-randomizes $\mathop{\text{Enc}}_{(a,b)}(x)$ (by decryption and encrypting with her key). The re-randomization is crucial so that the Bob does not learn which of $\mathop{\text{Enc}}_{(a,b)}(x)$ and $\mathop{\text{Enc}}_{(a,b)}\left( \overline{x} \right)$ is correct.

An example encryption function

There are many known commutative encryption schemes. See here for example. For completeness, we provide an example scheme that can work for our case. The downside for our simple method is that the size of the text grows linearly with the number of parties we want to be able to participate in the encryption.

The scheme depends on a cryptography sized group $G$ where discrete log is hard, and a known generator $g$ of the group.

• Setup: party $i$ computed a uniformly random number $x_i$, and computes $y_i = g^{x_i}$. $y_i$ is public, $x_i$ is not.

• Encryption: The encryption of the message is a triple $\left( g^{a_0},g^{a_1},my_0^{a_0}y_1^{a_1} \right)$.

  When a party (say party $0$) encrypts a plain text message $m$, they generate $a_0$ and compute the first and last element of the tuple, the middle element is left as $g^{0}$.

  If party $0$ encrypts triple (where the first element is the identity), they similarly generate $a_0$ to compute first element, then they multiply the last element by $y_0^{a_0}$. However, it’s important that they also randomize the coordinate associated with party $1$ (otherwise party $1$ might be able to identify the messages from their entry). To do they generate a random number $a'_1$, they multiply the middle element with $g^{a'_1}$, and the last element by $y_1^{a'_1}$

• Decryption: When party $0$ decrypts a message, $\left( t_1,t_2.t_3 \right) = \left( g^{a_0},g^{a_1},my_0^{a_0}y_1^{a_1} \right)$. They produce the tuple: $$\left( 1,t_2,t_3t_1^{- x_0} \right) = \left( 1,g^{a_1},my_1^{a_1} \right).$$ We see that if both parties decrypt the tuple, then $t_1 = t_2 = 1$, and the tuple is $(1,1,m)$ which allows them to read the message.

We leave it as exercise to the reader to see how this can extend to more than two parties by increasing the size of the tuple

Security Assumptions

Security against passive attacks

When using an IND-CPA secure encryption scheme, the protocol above does not reveal any information on the intermediate values (other than the final output). We can check this for each of our gate types:

1. Two known values: Security follows from the security of Oblivious Transfer.

2. One known values: Since the scheme is IND-CPA secure and the party who knows one of the values (Alice) re-randomizes the encryption, then other party (Bob) can not infer Alice’s bit because he can not distinguish the different message types ($0$, $1$, $e$, $\overline{e}$).

3. Zero known values: In this case, the random order of revealing $\mathsf{enc}$ and $\overline{\mathsf{enc}}$ makes it so that Bob can not learn anything about $\mathsf{enc}$ until the point Alice picks the “correct” output. However, since Alice re-encrypts the output. Bob learns nothing by IND-CPA. Alice learns nothing from the safety of “one known value” gates.

The correctness of our scheme relies on the encryption being commutative.

An active attack

One kind of attack that’s possible in our scheme but not possible when we use oblivious transfer on the whole table of possible outputs is that Alice (or Bob) could give two different gates different values of $a_1$. Depending on the structure of the circuit this might allow either Alice learn something it was not supposed to learn about Bob’s value (since this gives her control over more bits than the number of bits in her input).

Multiple parties

We leave it as an exercise to the reader to check that this scheme works for $k$ parties as follows:

1. When one of the input bits to the gate is known by at least some party, same scheme as above.

2. When both inputs are encrypted. One of the inputs (the pair $\left( e,\overline{e} \right)$) is decrypted and randomly permuted by a sequence of $k - 1$ of the parties, then the output is computed by the last party.

Note that the number of rounds per gate increases $O(k)$, though it is possible to get around by having the intermediate values encrypted by a subset of the parties (say $k'$). (This decreases the rounds at the expense of making $k'$ of the parties able to reveal intermediate values if they collude.)